 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 700 点
問題文
高橋君と青木君は、縦 H マス、横 W マスの透明な方眼紙を 1 枚ずつ手に入れました。
高橋君は、自分の方眼紙のいくつかのマスを赤く塗りました。 このとき、赤いマスは上下左右に連結でした。 つまり、どの赤いマスからどの赤いマスへも、上下左右に隣り合う赤いマスのみを辿って行き来できます。
また、青木君は、自分の方眼紙のいくつかのマスを青く塗りました。 このとき、青いマスは上下左右に連結でした。
その後、高橋君と青木君は、2 枚の方眼紙をそのままの向きでぴったりと重ねました。 すると、赤いマスと青いマスが重なるマスのみが紫色になって見えました。
紫色のマスの配置が、長方形に並ぶ文字 a_{ij} (1≤i≤H,1≤j≤W) として与えられます。
上から i 行目、左から j 列目のマスが紫色ならば、a_{ij} は # であり、紫色でなければ、a_{ij} は . です。
このとき、最も外側のマスは紫色でないことが保証されます。
つまり、i=1,H または j=1,W ならば、a_{ij} は . です。
問題文の条件を満たすような、赤いマスの配置と青いマスの配置のペアをひとつ求めてください。 解は必ず存在することが示せます。
制約
- 3≤H,W≤500
- a_{ij} は
#または.である。 - i=1,H または j=1,W ならば、a_{ij} は
.である。 - a_{ij} のうち少なくとも 1 つは
#である。
入力
入力は以下の形式で標準入力から与えられる。
H W
a_{11}...a_{1W}
:
a_{H1}...a_{HW}
出力
問題文の条件を満たすような、赤いマスの配置と青いマスの配置のペアをひとつ出力せよ。
- 1 行目から H 行目までには、赤いマスの配置を出力せよ。
- H+1 行目には、空行を出力せよ。
- H+2 行目から 2H+1 行目までには、青いマスの配置を出力せよ。
どちらも、紫色のマスの配置と同様のフォーマットで出力せよ。
入力例 1
5 5 ..... .#.#. ..... .#.#. .....
出力例 1
..... ##### #.... ##### ..... .###. .#.#. .#.#. .#.#. .....
例えば、次のような赤いマスの配置と青いマスの配置のペアが考えられます。
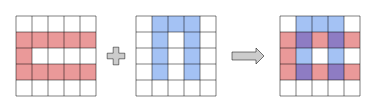
入力例 2
7 13 ............. .###.###.###. .#.#.#...#... .###.#...#... .#.#.#.#.#... .#.#.###.###. .............
出力例 2
............. .###########. .###.###.###. .###.###.###. .###.###.###. .###.###.###. ............. ............. .###.###.###. .#.#.#...#... .###.#...#... .#.#.#.#.#... .#.#########. .............
例えば、次のような赤いマスの配置と青いマスの配置のペアが考えられます。

Score : 700 points
Problem Statement
Snuke and Ciel went to a strange stationery store. Each of them got a transparent graph paper with H rows and W columns.
Snuke painted some of the cells red in his paper. Here, the cells painted red were 4-connected, that is, it was possible to traverse from any red cell to any other red cell, by moving to vertically or horizontally adjacent red cells only.
Ciel painted some of the cells blue in her paper. Here, the cells painted blue were 4-connected.
Afterwards, they precisely overlaid the two sheets in the same direction. Then, the intersection of the red cells and the blue cells appeared purple.
You are given a matrix of letters a_{ij} (1≤i≤H, 1≤j≤W) that describes the positions of the purple cells. If the cell at the i-th row and j-th column is purple, then a_{ij} is #, otherwise a_{ij} is .. Here, it is guaranteed that no outermost cell is purple. That is, if i=1, H or j = 1, W, then a_{ij} is ..
Find a pair of the set of the positions of the red cells and the blue cells that is consistent with the situation described. It can be shown that a solution always exists.
Constraints
- 3≤H,W≤500
- a_{ij} is
#or.. - If i=1,H or j=1,W, then a_{ij} is
.. - At least one of a_{ij} is
#.
Input
The input is given from Standard Input in the following format:
H W
a_{11}...a_{1W}
:
a_{H1}...a_{HW}
Output
Print a pair of the set of the positions of the red cells and the blue cells that is consistent with the situation, as follows:
- The first H lines should describe the positions of the red cells.
- The following 1 line should be empty.
- The following H lines should describe the positions of the blue cells.
The description of the positions of the red or blue cells should follow the format of the description of the positions of the purple cells.
Sample Input 1
5 5 ..... .#.#. ..... .#.#. .....
Sample Output 1
..... ##### #.... ##### ..... .###. .#.#. .#.#. .#.#. .....
One possible pair of the set of the positions of the red cells and the blue cells is as follows:

Sample Input 2
7 13 ............. .###.###.###. .#.#.#...#... .###.#...#... .#.#.#.#.#... .#.#.###.###. .............
Sample Output 2
............. .###########. .###.###.###. .###.###.###. .###.###.###. .###.###.###. ............. ............. .###.###.###. .#.#.#...#... .###.#...#... .#.#.#.#.#... .#.#########. .............
One possible pair of the set of the positions of the red cells and the blue cells is as follows:
