 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 2200 点
問題文
N 頂点 M 辺の無向グラフがあります。 ただし、N-1≤M≤N であり、グラフは連結です。 また、グラフには自己ループや多重辺はありません。
頂点は 1 から N まで番号が振られており、辺は 1 から M まで番号が振られています。 辺 i は頂点 a_i と b_i を結んでいます。
各頂点は白または黒になることができます。 最初、すべての頂点は白です。 高橋君は次の操作を何回か行い、すべての頂点を黒にしようとしています。
- 隣り合う同色の頂点のペアを選び、それらの色をともに反転する。 すなわち、ともに白ならばともに黒へ変え、ともに黒ならばともに白へ変える。
すべての頂点を黒にすることができるか判定し、できるならば必要な操作回数の最小値を求めてください。
制約
- 2≤N≤10^5
- N-1≤M≤N
- 1≤a_i,b_i≤N
- グラフには自己ループや多重辺はない。
- グラフは連結である。
部分点
- 1500 点分のデータセットでは、M=N-1 が成り立つ。
入力
入力は以下の形式で標準入力から与えられる。
N M a_1 b_1 a_2 b_2 : a_M b_M
出力
すべての頂点を黒にすることができるならば、必要な操作回数の最小値を出力せよ。
できないならば、代わりに -1 を出力せよ。
入力例 1
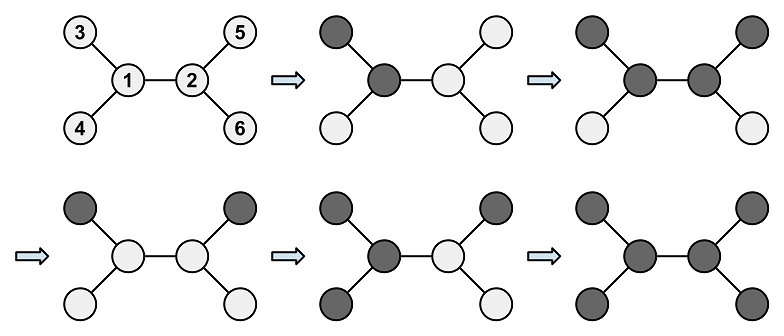
6 5 1 2 1 3 1 4 2 5 2 6
出力例 1
5
例えば、図のように操作を行えばよいです。
入力例 2
3 2 1 2 2 3
出力例 2
-1
すべての頂点を黒にすることはできません。
入力例 3
4 4 1 2 2 3 3 4 4 1
出力例 3
2
このケースは部分点のデータセットには含まれません。
入力例 4
6 6 1 2 2 3 3 1 1 4 1 5 1 6
出力例 4
7
このケースは部分点のデータセットには含まれません。
Score : 2200 points
Problem Statement
You are given an undirected graph with N vertices and M edges. Here, N-1≤M≤N holds and the graph is connected. There are no self-loops or multiple edges in this graph.
The vertices are numbered 1 through N, and the edges are numbered 1 through M. Edge i connects vertices a_i and b_i.
The color of each vertex can be either white or black. Initially, all the vertices are white. Snuke is trying to turn all the vertices black by performing the following operation some number of times:
- Select a pair of adjacent vertices with the same color, and invert the colors of those vertices. That is, if the vertices are both white, then turn them black, and vice versa.
Determine if it is possible to turn all the vertices black. If the answer is positive, find the minimum number of times the operation needs to be performed in order to achieve the objective.
Constraints
- 2≤N≤10^5
- N-1≤M≤N
- 1≤a_i,b_i≤N
- There are no self-loops or multiple edges in the given graph.
- The given graph is connected.
Partial Score
- In the test set worth 1500 points, M=N-1.
Input
The input is given from Standard Input in the following format:
N M a_1 b_1 a_2 b_2 : a_M b_M
Output
If it is possible to turn all the vertices black, print the minimum number of times the operation needs to be performed in order to achieve the objective.
Otherwise, print -1 instead.
Sample Input 1
6 5 1 2 1 3 1 4 2 5 2 6
Sample Output 1
5
For example, it is possible to perform the operations as shown in the following diagram:

Sample Input 2
3 2 1 2 2 3
Sample Output 2
-1
It is not possible to turn all the vertices black.

Sample Input 3
4 4 1 2 2 3 3 4 4 1
Sample Output 3
2
This case is not included in the test set for the partial score.

Sample Input 4
6 6 1 2 2 3 3 1 1 4 1 5 1 6
Sample Output 4
7
This case is not included in the test set for the partial score.
